Wiener Filter

为什么需要Wiener Filter?

图像重构的过程中会引入噪音。一种噪音在频域与源信号是分开的，可以通过滤波将其去掉；另一种噪音和源信号混合在一起，需要通过概率的方法估计得到恢复信号。

第二种噪音的去除可以通过Wiener滤波器实现。

如下图所示滤波之后引入了噪音 $g(\boldsymbol{n})=s(\boldsymbol{n})*h(\boldsymbol{n})+v(\boldsymbol{n})$

通过估计方法得到恢复信号：

$\hat{s}(\boldsymbol{n})=[s(\boldsymbol{n})*h(\boldsymbol{n})+v(\boldsymbol{n})]*h^I(\boldsymbol{n})$

转化到频域：

$\hat{S}_\delta(\boldsymbol{f})=S_\delta(\boldsymbol{f})\cdot H_\delta(\boldsymbol{f})\cdot H_\delta^I(\boldsymbol{f})+V_\delta(\boldsymbol{f})\cdot H_\delta^I(\boldsymbol{f})$

产生的误差：

$E_\delta(\boldsymbol{f})=V_\delta(\boldsymbol{f})\cdot H_\delta^I(\boldsymbol{f})$

可以看到误差 $E_\delta(\boldsymbol{f})$ 受 $H_\delta^I(\boldsymbol{f})$ 的影响很大。也就是说，滤波后的误差V(n)会在重构的过程中被放大。所以我们不能直接用H的逆变换来恢复图像，而是改为采用Wiener Filter。简单来说Wiener Filter就是把 $H_\delta^I(\boldsymbol{f})$ 进行改造，从而减小误差的影响。

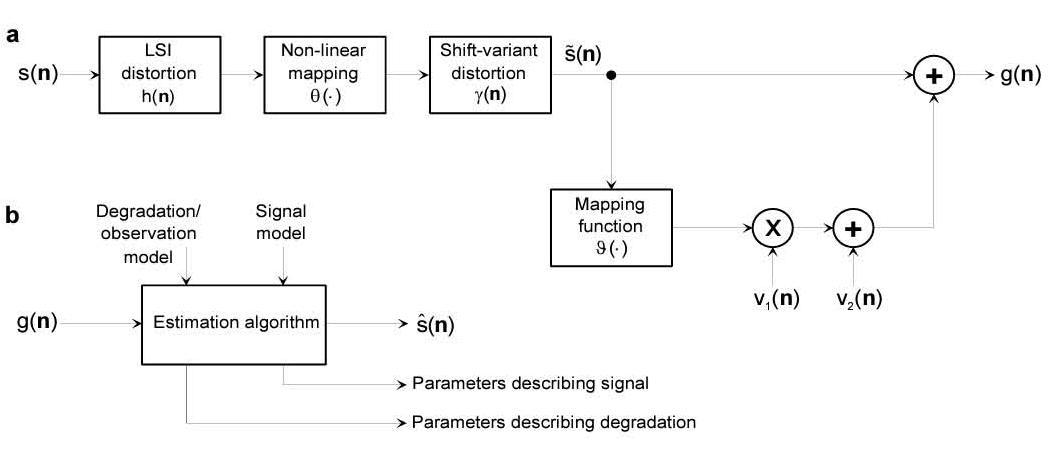
a)滤波 b)恢复

原图和通过低通滤波器的图像对比

如何得到Wiener Filter

下面介绍Wiener Filter的原理（即如何找到新的 $H_\delta^I(\boldsymbol{f})$）：

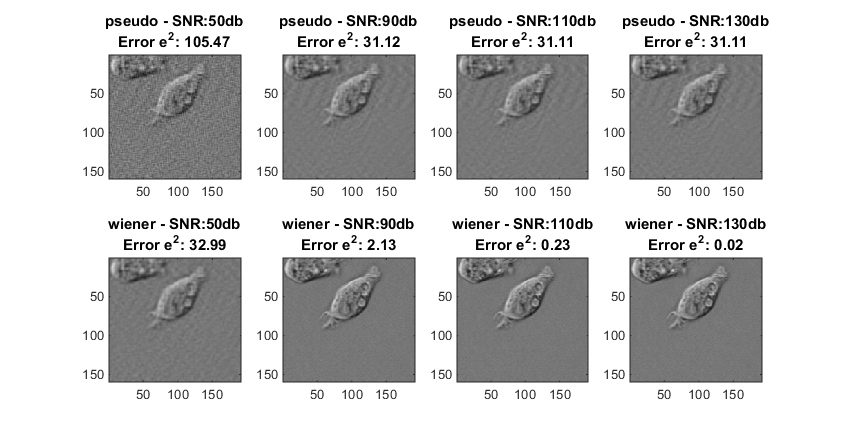
Inverse Filter与Wiener Fileter在不同程度的噪音下恢复得到的图像